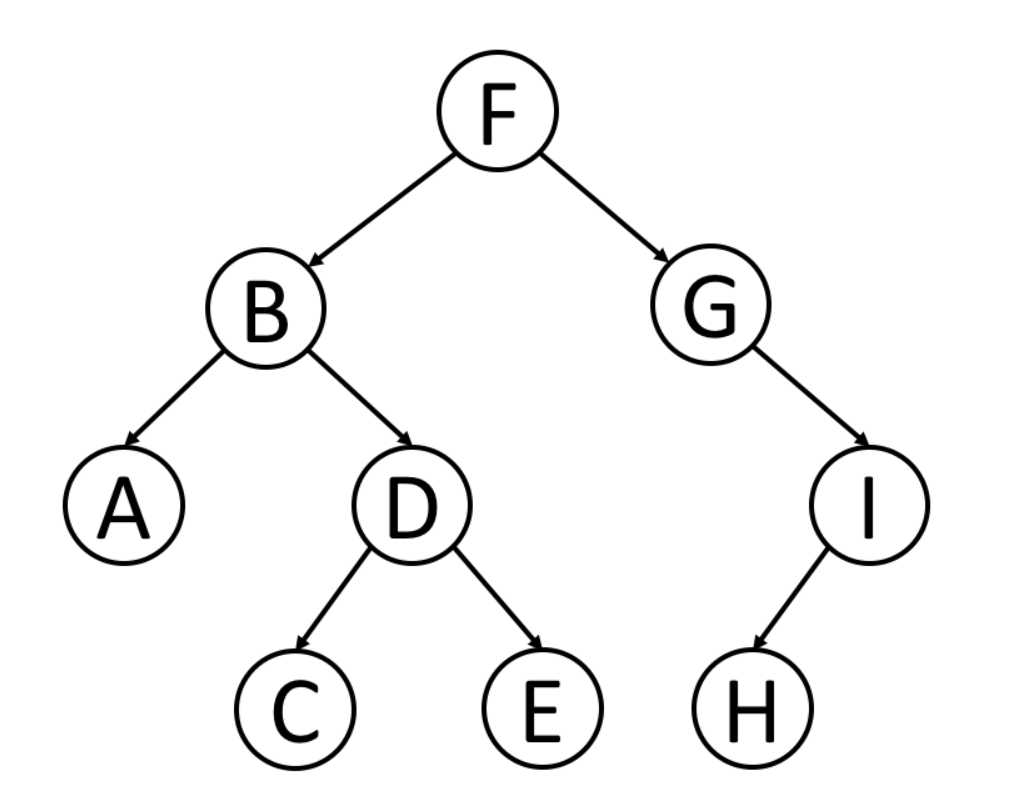
数据结构与算法之二叉树

二叉树

//Definition for a binary tree node.
public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right; 
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

二叉树的遍历

前序遍历

先访问树的根节点然后遍历左子树最后遍历右子树

中序遍历

先遍历左子树然后访问树的根节点最后遍历右子树

后序遍历

先遍历左子树然后遍历右子树最后访问树的根节点

class Solution {
    public List<Integer> orderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        traverse(root, res);
        return res;
    }

    public void traverse(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
       //res.add(root.val);   前序遍历
        traverse(root.left, res);
       //res.add(root.val);   中序遍历
        traverse(root.right, res);
       //res.add(root.val);   后序遍历
    }
}

特点：前序遍历第一个元素是root节点

层次遍历

二叉树的经典问题

翻转；判断是否对称；

二叉搜索树

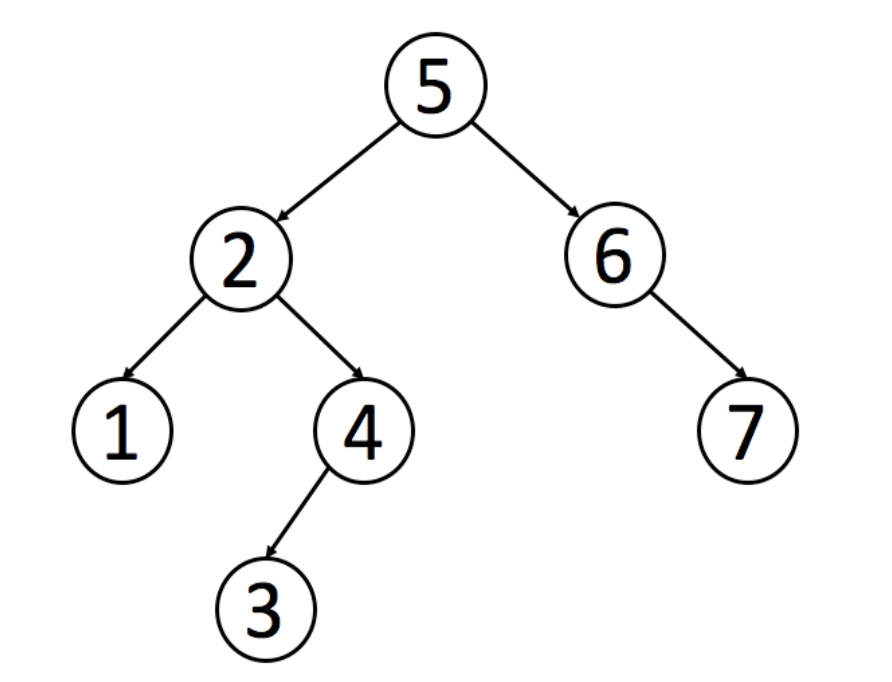
定义：

节点左子树只包含小于当前节点的数
节点右子树只包含大于当前节点的数
左子树和右子树也必须是二叉搜索树

二叉树的中序遍历是一个升序

public void traverse(TreeNode root, List<Integer> res) {
    if (root == null) {
        return;
    }  
    traverse(root.left, res);
   //res.add(root.val);   中序遍历
    traverse(root.right, res);
}

要降序该如何处理中序遍历时交换 traverse(root.left, res)和 traverse(root.right, res)的顺序

public void traverse(TreeNode root, List<Integer> res) {
    if (root == null) {
        return;
    }  
    traverse(root.right, res);
    //res.add(root.val);   中序遍历
    traverse(root.left, res);
}

常见面试题验证一棵树为二叉搜索树，BST的搜索、插入、删除操作

验证BST

BST的搜索

public TreeNode searchBST(TreeNode root, int val) {
  if (root == null) {
    return null;
  }
  if (root.val == val) {
    return root;
  } else if (root.val > val) {
    return searchBST(root.left, val);
  } else {
    return searchBST(root.right, val);
  }
}